The vessel design process progresses in stages, beginning with the definition of requirements and then advancing to concept design, which aims at understanding the key design trade-offs. In-depth understanding of the design problem at this early stage prevents locking in poor choices requiring costly changes later. While the conceptual-stage design of conventional vessels relies on statistical data from similar existing vessels, such data is often missing for new vessel concepts employing hybrid power source, hybrid propulsion or battery-electric configurations. For evaluating new concepts, first principles design models are needed. A mathematical program is a type of design model that outputs a design that achieves the specified requirements, while minimizing a given performance function.
In the general nonlinear programming approach typically used in naval architecture, a local search method is employed to seek a locally optimal point to the design problem. Using a local optimization method involves experimenting with the choice of the algorithm, adjusting algorithm parameters and starting the search from many different initial points. Even with proper choice of the algorithm by a skilled naval architect, the solution times for practical problems in the industry typically range from hours to days. Thus, the design space can be explored in only a few dimensions under the strict time limit imposed on the conceptual design stage.
In a recently published paper titled Design Optimization of Battery-electric Marine Vessels via Geometric Programming, researchers from Aalto University propose formulating the conceptual-stage design problem in a specific functional form, called a geometric program. The key advantage of formulating problems in this form is that they can then be solved extremely fast and reliably using standard numerical algorithms. Moreover, no algorithm selection, parameter tuning or guessing of initial points are needed. Although the geometric programming approach may appear too restrictive at first impression, the paper illustrates that the key design relationships can be formulated accurately within this framework.
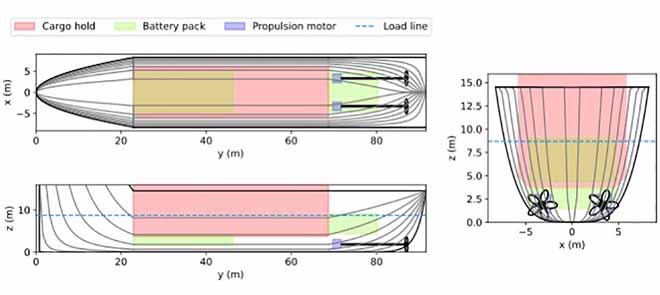
The paper presents a numerical example that seeks the minimum battery size for a battery-electric coastal bulk carrier sailing in varying operational conditions. In addition to powertrain component dimensioning, the study also considers preliminary hull form development, stability calculation and structural design. Using open-source software tools, the problem instances are solved in less than a second on a standard desktop computer. The study also illustrates another key advantage of the proposed geometric programming modeling approach: the solvers return optimal dual variables for free. The dual variables encode sensitivity information that is useful for guiding the naval architect to focus on the most impactful design decisions.
More about the topic: Ritari, A., Mouratidis, P., & Tammi, K. (2023). Design Optimization of Battery-Electric Marine Vessels via
Geometric Programming. IEEE Access, 11, 76563 – 76580. https://research.aalto.fi/files/117448807/gp_design.pdf
This work was supported by Clean Propulsion Technologies Research Project.